Skip to contents

S2a: Elements of PCA

Vincent J. Carey, stvjc at channing.harvard.edu

November 02, 2024

Source: vignettes/S2a_PCAelem.Rmd
S2a_PCAelem.Rmd

Overview

This vignette explores basic aspects of PCA in bivariate and 5-dimensional data. It concludes with some remarks about “eigengenes”, which can be verified using the computations shown in the simpler cases.

Make a bivariate dataset with positive correlation and heterogeneous variance

First we create a covariance matrix with greater variance for second variable of our pair.

library(MASS)
set.seed(1234)
options(digits=3)
cm = matrix(c(1,1,1,4), nr=2)
cm
##      [,1] [,2]
## [1,]    1    1
## [2,]    1    4

Then we generate a 20000 x 2 matrix of bivariate normal deviates.

sim1 = mvrnorm(20000, c(0,0), cm)
cov(sim1)
##       [,1]  [,2]
## [1,] 1.002 0.995
## [2,] 0.995 3.973
cor(sim1)
##       [,1]  [,2]
## [1,] 1.000 0.499
## [2,] 0.499 1.000

The data in the original units is easy to visualize:

plot(sim1,xlim=c(-10,10), ylim=c(-10,10))

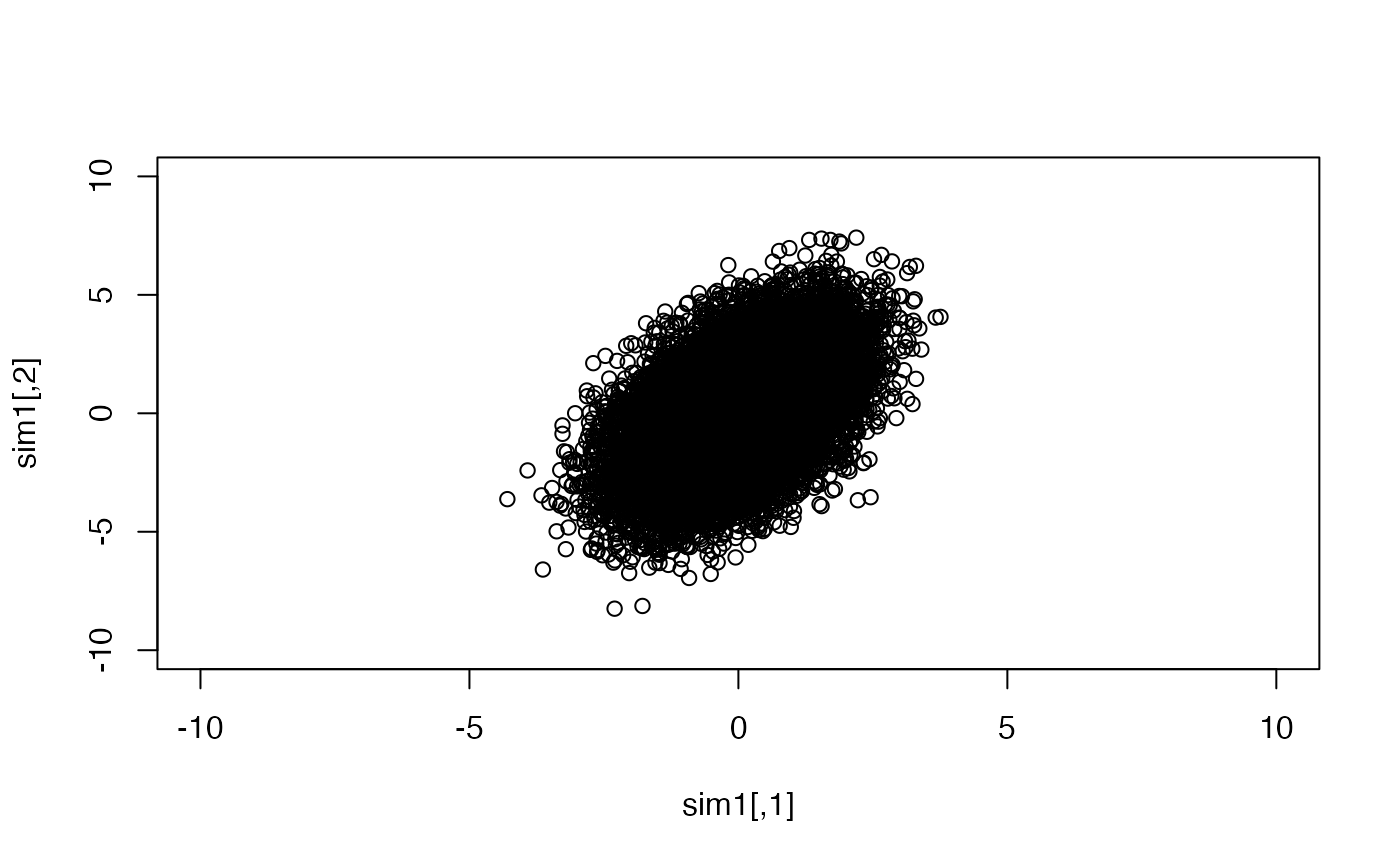
Now we will perform a PCA. We don’t have to reduce dimensions, but we can get a handle on how the components are formed and interpreted.

prc = prcomp(sim1, center=FALSE)
plot(prc$x, xlim=c(-10,10), ylim=c(-10,10))

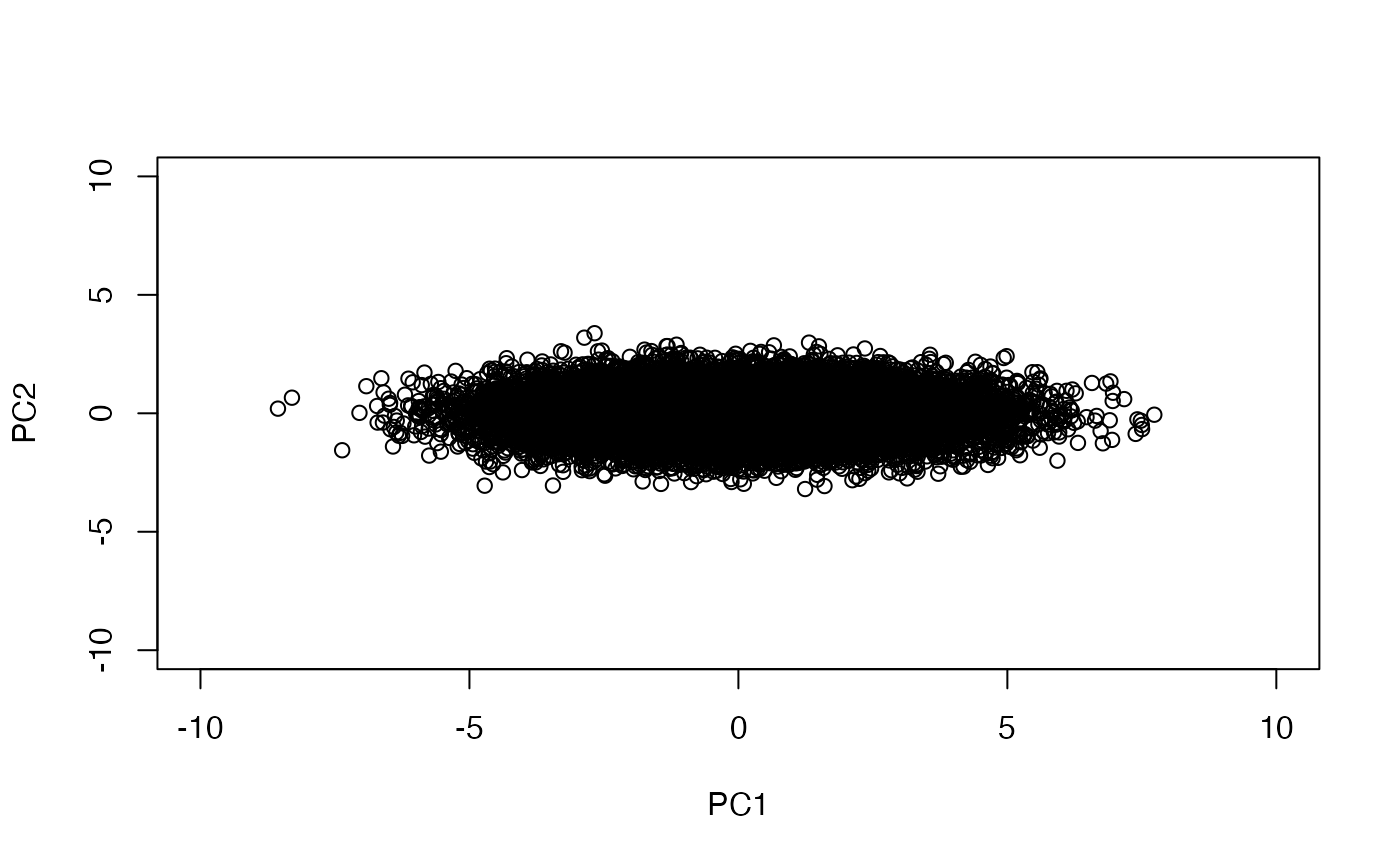
PC1 is produced by taking linear combinations of the rows of sim1.

We’ll illustrate the linear combination concept. The data vector for the first row may be written (x1,x2)(x_1, x_2), and a linear combination has the form ax1+bx2ax_1 + bx_2 for some coefficients aa and bb.

The coefficients are derived from the rotation component of the PCA.

prc$rotation
##        PC1    PC2
## [1,] 0.291  0.957
## [2,] 0.957 -0.291
c11 = prc$rotation[1,1]
c21 = prc$rotation[2,1]
sim1[1,1]*c11 + sim1[1,2]*c21
##  PC1 
## -2.5
prc$x[1,1]
##  PC1 
## -2.5

This can be done wholesale using matrix multiplication %*%:

(sim1 %*% prc$rotation)[1:5,]
##         PC1    PC2
## [1,] -2.502  1.412
## [2,]  0.576  0.797
## [3,]  2.250  0.539
## [4,] -4.866 -0.213
## [5,]  0.891  1.017
prc$x[1:5,]
##         PC1    PC2
## [1,] -2.502  1.412
## [2,]  0.576  0.797
## [3,]  2.250  0.539
## [4,] -4.866 -0.213
## [5,]  0.891  1.017
all.equal(prc$x, sim1%*% prc$rotation)
## [1] TRUE

Exercises.

  • Recover the value of prc$x[1,2] using the second column of prc$rotation.

  • Examine these plots

par(mfrow=c(2,2), mar=c(4,4,3,1))
plot(sim1, xlim=c(-10,10), ylim=c(-10,10), main="raw data",
  xlab="data column 1", ylab="data col. 2")
plot(sim1 %*% prc$rotation, xlim=c(-10,10), ylim=c(-10,10),
  main="data %*% prc$rotation", xlab="PC1 via rotation",
   ylab="PC2 via rotation")
plot(prc$x, xlim=c(-10,10), ylim=c(-10,10), main="x from prcomp",
    )
plot(sim1 %*% 
 prc$rotation %*% t(prc$rotation), xlim=c(-10,10), ylim=c(-10,10),
  main="data %*% rot %*% t(rot)", xlab="data %*% VVt (col 1)",
  ylab = "data %*% VVt (col 2)")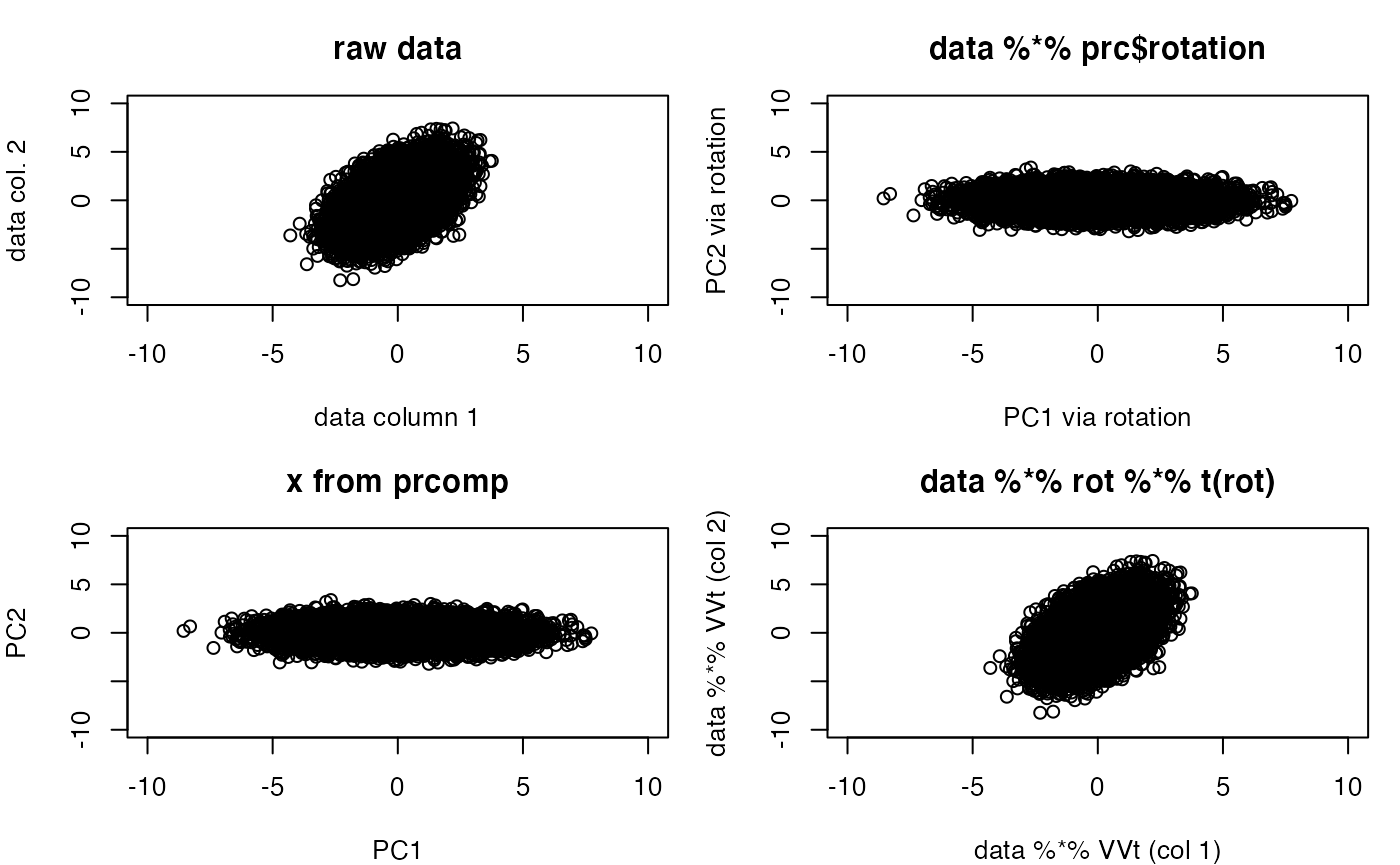

The rotation has been “undone”. Letting VV denote the ‘rotation’ component of the PCA, this shows that the matrix product VVt=IVV^t = I, where II is a diagonal matrix with 1 on the diagonal. More background on the underlying computations can be gleaned from the Wikipedia entry on singular value decomposition.

A larger covariance matrix

Here we have a 5-dimensional dataset. We set up the covariance matrix so that columns 1 and 2 have negative correlation, columns 3 and 4 have positive correlation, column 2 has greatest overall variance, and columns 1 and 3 have elevated variance.

cm = diag(5)
cm[3,4] = cm[4,3] = .8
cm[1,2] = cm[2,1] = -.6
A = diag(5)
A[1,1] = 2
A[2,2] = 3
A[3,3] = 2
covm = A%*%cm%*%A
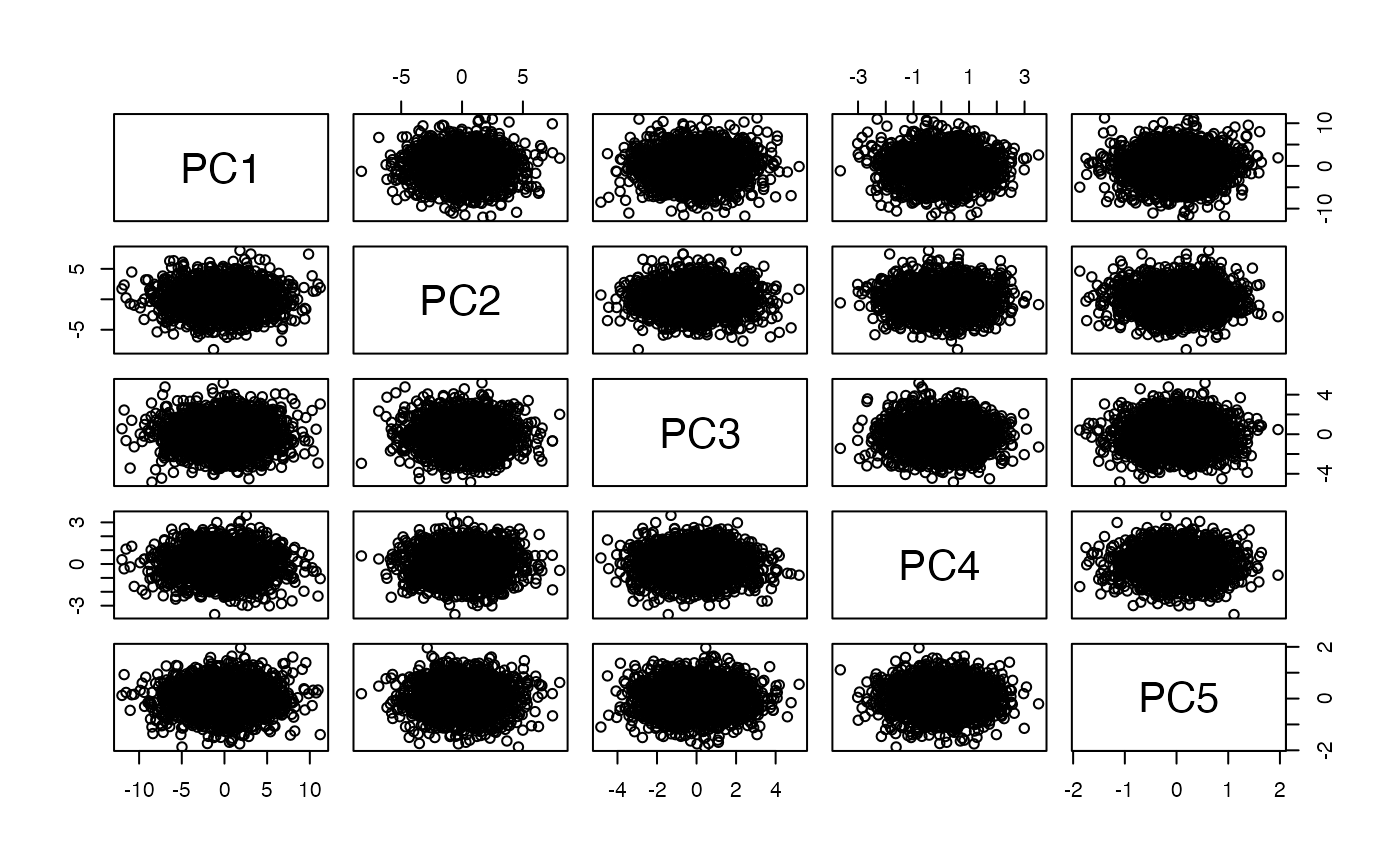
myd = mvrnorm(2000, rep(0,5), covm)

The pairs plot shows the data in original units.

pairs(myd, xlim=c(-10,10), ylim=c(-10,10))

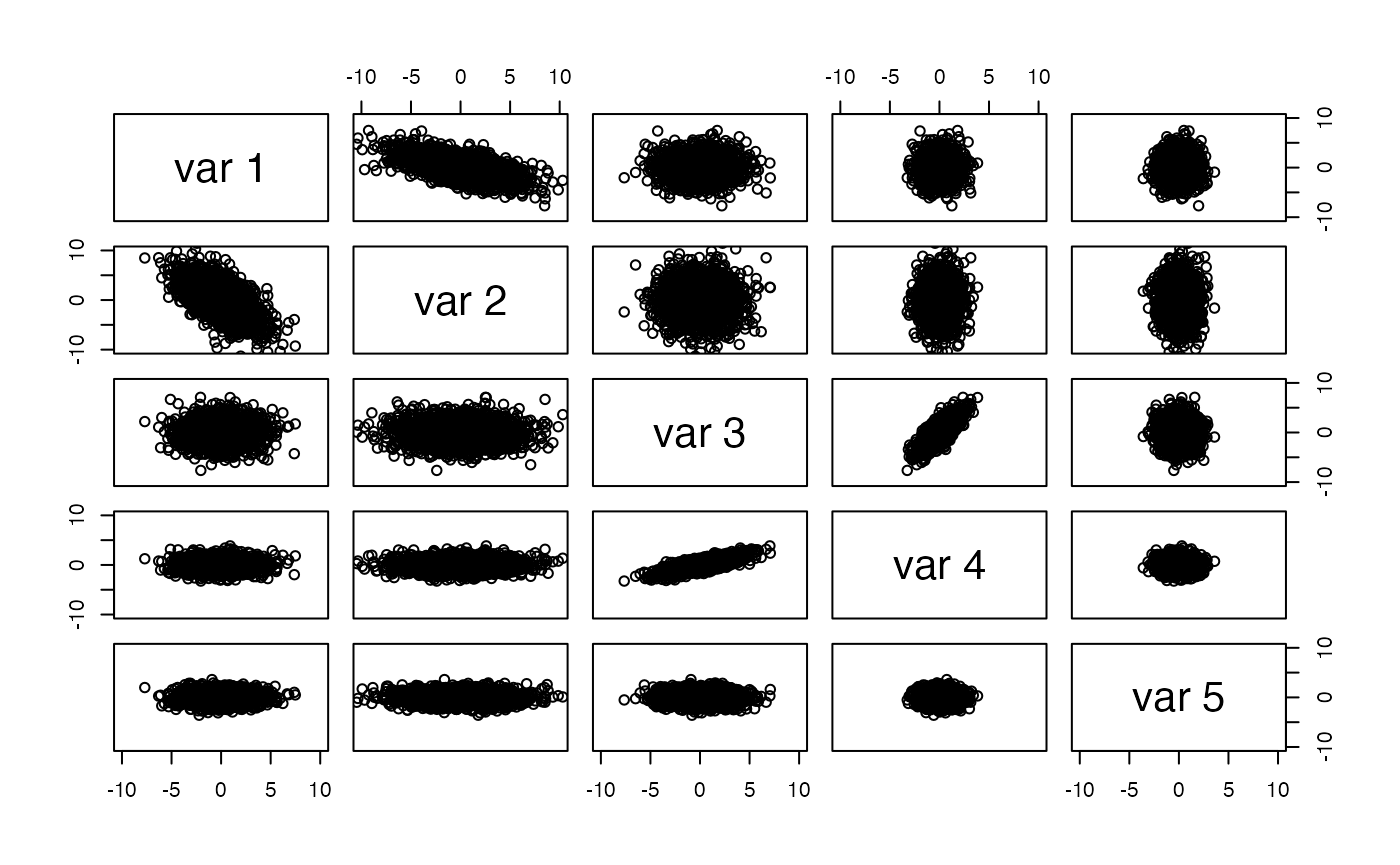
We verify the multivariate structure:

cor(myd)
##          [,1]     [,2]     [,3]     [,4]    [,5]
## [1,]  1.00000 -0.61123 -0.00337  0.01546  0.0489
## [2,] -0.61123  1.00000 -0.00105  0.00686 -0.0348
## [3,] -0.00337 -0.00105  1.00000  0.80438 -0.0361
## [4,]  0.01546  0.00686  0.80438  1.00000 -0.0365
## [5,]  0.04888 -0.03478 -0.03611 -0.03648  1.0000
cov(myd)
##         [,1]     [,2]     [,3]    [,4]    [,5]
## [1,]  4.1482 -3.88159 -0.01360  0.0317  0.0986
## [2,] -3.8816  9.72168 -0.00648  0.0215 -0.1075
## [3,] -0.0136 -0.00648  3.91911  1.6017 -0.0708
## [4,]  0.0317  0.02153  1.60174  1.0118 -0.0364
## [5,]  0.0986 -0.10745 -0.07082 -0.0364  0.9816
dim(myd)
## [1] 2000    5

Compute PCA

pp = prcomp(myd)
pairs(pp$x)

The biplot shows the projection to PC1-PC2 and shows how the different variables are related, and how they drive the projection.

par(lwd=2)
biplot(pp, xlabs=rep(".", 2000), expand=.8)

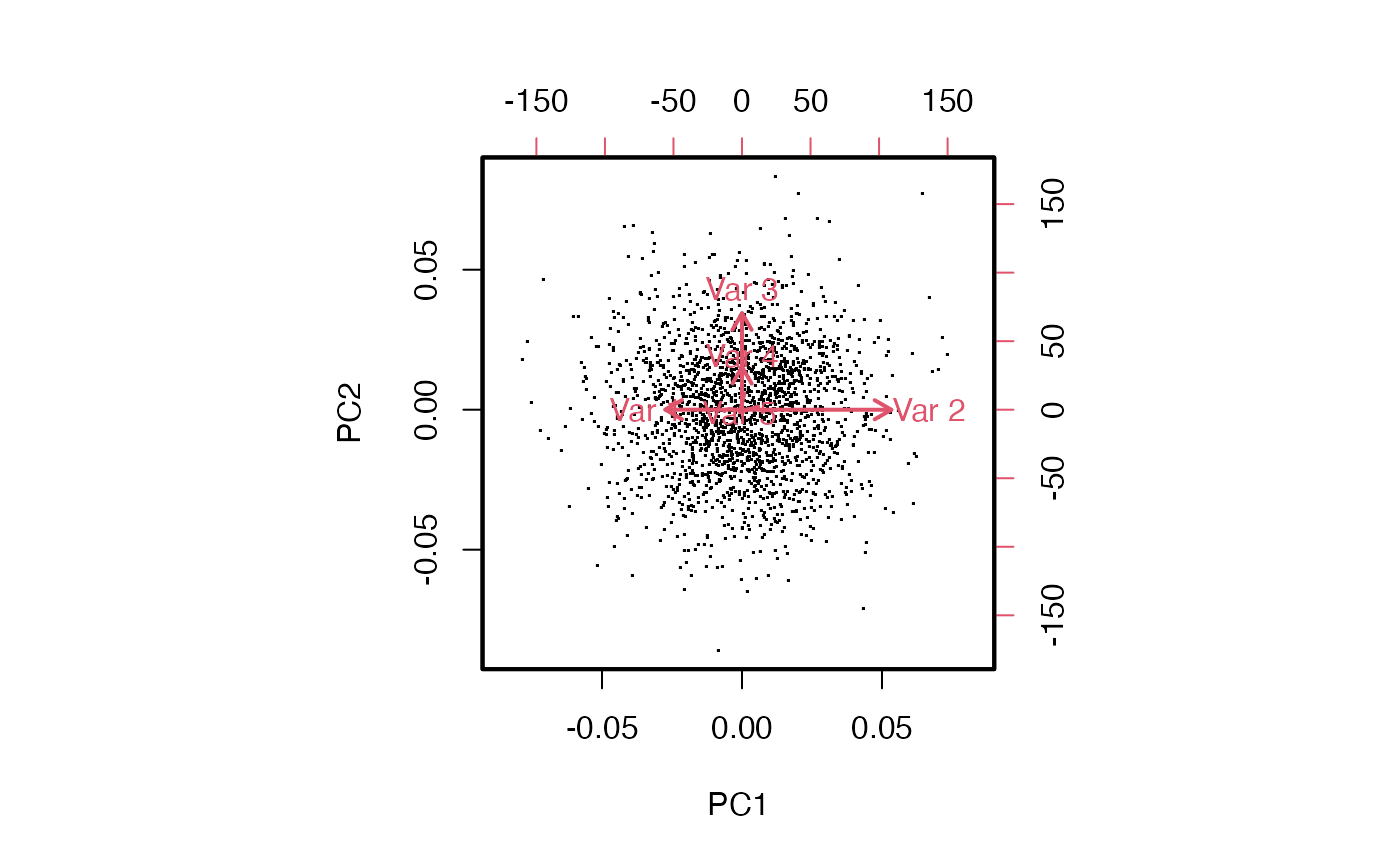
Exercise: Explain the configuration of arrows in the biplot.

“Eigengenes” derived from PCA

When the rows are samples and columns are genes, the x components of prcomp’s output are linear combinations of all genes. The coefficients of the combination are derived from the PCA rotation matrix, which is constructed so as to

  • order the PCs so that the components capturing the most variation come first
  • construct the PCs so they are mutually orthogonal

Note that the simple reconstructions above have required that prcomp be used with center=FALSE.